Equação é como chamamos uma sentença com uma igualdade, números, operações e letras.
Exemplo:
2x+3=8x
As letras da equação são chamadas incógnitas, que significa desconhecido, ou variáveis, já que podem assumir múltiplos valores até se ter certeza qual deles é.
Resolver uma equação corresponde a descobrir o valor da incógnita ou das incógnitas, se houver mais de uma. O processo ocorre, resumidamente, em três etapas básicas:
Resolver uma equação corresponde a descobrir o valor da incógnita ou das incógnitas, se houver mais de uma. O processo ocorre, resumidamente, em três etapas básicas:
- Aproximar os elementos semelhantes;
- Operar os semelhantes;
- Isolar a incógnita;
Antes de partir para a resolução de equações, é importante que se conheça os tipos delas, evitando menos confusão!
TIPOS DE EQUAÇÕES
1º Grau
2x=2-1 (Passamos o "1" para o 2º membro trocando seu sinal)
2x=1 (Subtraimos "1" de "2")
x=1/2 (Pegamos o "2" que estava multiplicando com o "x" e passamos para o 2º membro dividindo o "1", RESOLVIDO ou podemos dividir o "1" por "2" dando "0,5")
Exemplo:
Equação de 1º grau é aquela cujo maior expoente de uma incógnita qualquer é 1 (é quando temos a letra sem expoente algum, nesse caso seu expoente é 1). Ver exemplo:
2x+1=2
O que está do lado esquerdo do sinal de igual é chamado 1º membro, o que está do lado direito, é chamado 2º membro.
O passo a passo da resolução da equação acima é:2x=2-1 (Passamos o "1" para o 2º membro trocando seu sinal)
2x=1 (Subtraimos "1" de "2")
x=1/2 (Pegamos o "2" que estava multiplicando com o "x" e passamos para o 2º membro dividindo o "1", RESOLVIDO ou podemos dividir o "1" por "2" dando "0,5")
3x-1 = 3+4x
Resolução:
3x-4x=3+1 (Os números encostados em letras iguais com o mesmo expoente são semelhantes entre si, os sem letra, chamados termos independentes, são semelhantes entre si. Os semelhantes devem ser aproximados com inversão de sinal se "saltarem" a igualdade)
-x=4 * (-1) ("3x-4x" dá "-x", pois "3" é positivo e "-4" é negativo, sinais diferentes subtrai e dá o sinal do maior, repetindo o "x". Quando se faz as operações, faz-se apenas com os coeficientes numéricos, os números encostados nas letras iguais de mesmo expoente, estas são chamadas parte literal, e repetimos as letras. O "1" encostado na letra pode ser ocultado. Agora, multiplicamos toda a equação por "-1" para "x" ficar positivo)
x= - 4 (Resolvido)
2º grau
2º grau
Equação de segundo grau, quadrada ou quadrática, como também é conhecida, tem o maior expoente de qualquer incógnita dela como sendo dois.
Exemplo:
2x²+3x-8 = 0
Acima você vê um exemplo de uma equação de segundo grau. Perceba que "x" aparece duas vezes e analisando as duas, vemos que seu maior expoente é 2, então esta equação é de segundo grau.
Para resolver uma dessas, veja a forma genérica dela antes:
ax²+bx+c = 0
Como podemos ver, ela é composta por duas partes. A debaixo calcula o delta e vai na raiz da de cima.
Para usar esta fórmula, você tem que pegar cada coeficiente da equação de 2º grau conforme a forma genérica, isto é, tem que pegar "a", "b" e "c" da equação e ir substituindo nos seus devidos lugares nas duas fórmulas aí em cima.
É recomendado começar sempre pelo cálculo do delta, pois, dependendo do resultado, pode ser que você não precise mais continuar o processo. Equações de 2º grau, podem ter três resultados possíveis: dois diferentes ou dois iguais para a incógnita ou nenhum resultado, ou seja:
1ª) Delta negativo: se ocorrer este caso, não haverá nenhum valor real para a incógnita, pois ao colocarmos o valor de delta na fórmula de Bhaskara, teremos que obter uma raiz quadrada de número negativo e isso não existe para o conjunto dos números Reais normalmente abrangido por esta fórmula.
2ª) Delta nulo: se ocorrer este caso, a incógnita assumirá dois valores iguais; em palavras mais simples, um único resultado.
3ª) Delta positivo: neste caso, a incógnita terá dois valores diferentes.
3ª) Delta positivo: neste caso, a incógnita terá dois valores diferentes.
Vamos fazer um exemplo de cada caso:
1ª) 2x²-x+4 = 0
a = 2
b = -1
c = 4
Como podemos observar ao lado, o delta deu resultado negativo, assim, nosso cálculo para por aqui mesmo e o conjunto solução é:
S={ };
2ª) 2x²-4x+2=0
a = 2
b = -4
c = 2
(Substituição dos valores dos coeficientes na fórmula de Bhaskara. Como Delta é nulo, x1 é igual a x2.)
a = 2
b = -4
c = 2
Neste caso, o delta deu nulo, assim, pouco importa se o sinal é negativo ou não antes da raiz, pois somando ou subtraindo nada de alguma coisa, continua a mesma alguma coisa. Acompanhe o cálculo abaixo:
(Substituição dos valores dos coeficientes na fórmula de Bhaskara. Como Delta é nulo, x1 é igual a x2.)
(Esquecemos a raiz quadrada e fazemos jogo de sinal com os parênteses ficando "4" positivo)
(Resultado)
3ª) 3x²-x-4=0
a = 3
b = -1
c = -4
(Cálculo da raiz quadrada, eliminação dos parênteses fazendo jogo de sinais e multiplicação no denominador)
(Simplificação)
(Resultado)
Conjunto solução:
a = 3
b = -1
c = -4
Vemos que o delta deu positivo, portanto há dois valores possíveis para a incógnita, o que nos obriga a continuar com o cálculo.
(Substituição dos valores dos coeficientes usando o sinal positivo antes da raiz)
(Cálculo da raiz quadrada, eliminação dos parênteses fazendo jogo de sinais e multiplicação no denominador)
(Simplificação)
(Resultado)
(Cálculo da raiz quadrada, eliminação dos parênteses fazendo jogo de sinais e multiplicação no denominador)
(Divisão)
(Resultado)
Conjunto solução:
S={-1;4/3}

Feitas as operações com os semelhantes, entre parênteses, separamos o "x²" (lembre-se que x elevada a quarta potência é o mesmo que x elevado ao quadrado duas vezes.).
Adotamos "y" sendo igual a "x²" e substituímos na equação, puxando o "-2" para o 1º membro.
Pegamos a fórmula do delta da equação de 2º grau, que é o que temos agora, e substituímos os valores de "a", "b" e "c" dela.
Resolvemos o delta normalmente como já sabemos e descobrimos que ele dá positivo, então teremos que prosseguir com o cálculo.
Jogamos os valores do delta e de "b" e "a".
Com o 7 fazemos o jogo de sinais e ele fica positivo. Embaixo multiplicamos o 2 com o 3, ficando 6.
Primeiro obtemos a raiz quadrada de 25 que é 5, porém tanto 5 positivo quanto 5 negativo elevados ao quadrado dão 25, por isso temos esse mais e menos entre 7 e 5.
Dividimos o cálculo agora em duas seções: uma com y1 em que ficamos com o sinal de mais entre 7 e 5; e outra com y2 em que ficamos com o sinal de menos entre 7 e 5.
Acima realizamos as operações de praxe como somar, subtrair, dividir e, quando necessário, simplificar.
Ainda na imagem anterior, descobrimos o valor de cada y, igualamos cada um ao x² de antes, com um índice para separarmos os resultados.
 Passando o expoente do x para o 2º membro, ele vira uma raiz que pede duas respostas, para cada x, e cada resposta terá dois sinais: um positivo e outro negativo.
Passando o expoente do x para o 2º membro, ele vira uma raiz que pede duas respostas, para cada x, e cada resposta terá dois sinais: um positivo e outro negativo.

Nada podemos fazer com o x1, mas com o x2 sim. Neste colocamos raízes no numerador e no denominador e logo em seguida racionalizamos.
Com a racionalização, multiplicamos o numerador e o denominador pelo racional que este contém, assim, ele sobe para o numerador e embaixo temos apenas a raiz de nove que é 3.
Vejamos abaixo o conjunto solução da nossa equação:
Equação biquadrada
Equação biquadrada é de 4º grau, portanto, corresponde a de 2º grau ao quadrado.
É um pouco mais complicado resolvê-la, mas nada que usando nossa "Sapiência" não consigamos desenrolar. Vejamos sua forma genérica:
Observando a forma genérica acima, vemos que é obrigatório a incógnita, no caso "x", ter expoentes pares. Vamos a resolução de uma:
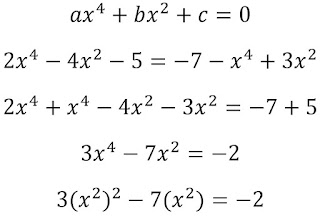 Inicialmente temos uma equação toda bagunçada que devemos organizar juntando os semelhantes, lembrando de mudar o sinal do elemento quando passar a igualdade.
Inicialmente temos uma equação toda bagunçada que devemos organizar juntando os semelhantes, lembrando de mudar o sinal do elemento quando passar a igualdade.
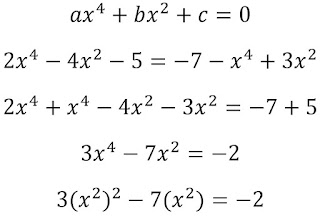 Inicialmente temos uma equação toda bagunçada que devemos organizar juntando os semelhantes, lembrando de mudar o sinal do elemento quando passar a igualdade.
Inicialmente temos uma equação toda bagunçada que devemos organizar juntando os semelhantes, lembrando de mudar o sinal do elemento quando passar a igualdade.
Feitas as operações com os semelhantes, entre parênteses, separamos o "x²" (lembre-se que x elevada a quarta potência é o mesmo que x elevado ao quadrado duas vezes.).
Adotamos "y" sendo igual a "x²" e substituímos na equação, puxando o "-2" para o 1º membro.
Pegamos a fórmula do delta da equação de 2º grau, que é o que temos agora, e substituímos os valores de "a", "b" e "c" dela.
Resolvemos o delta normalmente como já sabemos e descobrimos que ele dá positivo, então teremos que prosseguir com o cálculo.
Jogamos os valores do delta e de "b" e "a".
Com o 7 fazemos o jogo de sinais e ele fica positivo. Embaixo multiplicamos o 2 com o 3, ficando 6.
Primeiro obtemos a raiz quadrada de 25 que é 5, porém tanto 5 positivo quanto 5 negativo elevados ao quadrado dão 25, por isso temos esse mais e menos entre 7 e 5.
Dividimos o cálculo agora em duas seções: uma com y1 em que ficamos com o sinal de mais entre 7 e 5; e outra com y2 em que ficamos com o sinal de menos entre 7 e 5.
Acima realizamos as operações de praxe como somar, subtrair, dividir e, quando necessário, simplificar.
Ainda na imagem anterior, descobrimos o valor de cada y, igualamos cada um ao x² de antes, com um índice para separarmos os resultados.
 Passando o expoente do x para o 2º membro, ele vira uma raiz que pede duas respostas, para cada x, e cada resposta terá dois sinais: um positivo e outro negativo.
Passando o expoente do x para o 2º membro, ele vira uma raiz que pede duas respostas, para cada x, e cada resposta terá dois sinais: um positivo e outro negativo.
Nada podemos fazer com o x1, mas com o x2 sim. Neste colocamos raízes no numerador e no denominador e logo em seguida racionalizamos.
Com a racionalização, multiplicamos o numerador e o denominador pelo racional que este contém, assim, ele sobe para o numerador e embaixo temos apenas a raiz de nove que é 3.
Vejamos abaixo o conjunto solução da nossa equação:
Veja que tivemos quatro raízes diferentes. É sempre assim? Vai depender do delta. Se ele for positivo a equação biquadrada vai ter 4 raízes distintas, diferentes. Se der nulo, terá apenas duas distintas e, se der negativo, a equação não terá nenhuma, isso dentro do Conjunto dos Números Reais.























